Antonio Morais: A Bayesian approach to machine learning model comparison
Posted on Mon 28 February 2022 in theses
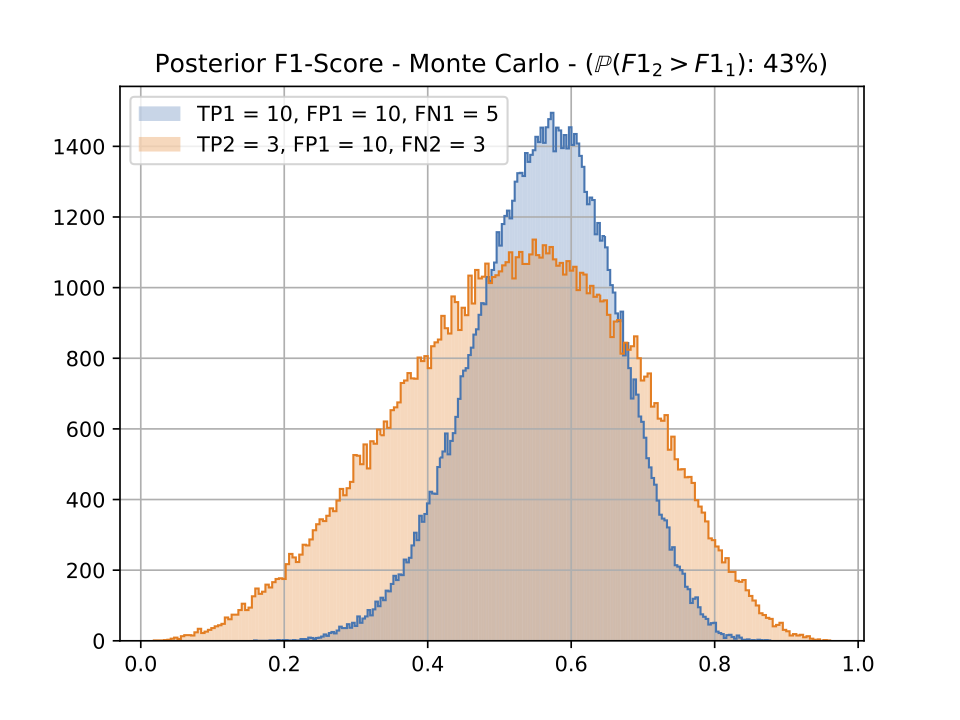
In this figure, we can see the distribution generation produced by the Monte Carlo simulation. If we only computed the F1-score using the usual formula we would have 0.571 for the first system and 0.315 for the second one so we would conclude that system 1 is way better than system 2. The probabilistic outlook gives another point of view. Even though the first model seems preferable as it is more consistent and has a better mode and average, the second model does not seem that far, and actually outperforms system 1 in 43% of the cases.
Performance measures are an important component of machine learning algorithms. They are useful when it comes to evaluate the quality of a model, but also to help the algorithm improve itself. Every need has its own metric. However, when we have a small data set, these measures don’t express properly the performance of the model. That’s when confidence intervals and credible regions come in handy. Expressing the performance measures in a probabilistic setting lets us develop them as distributions. Then we can use those distributions to establish credible regions. In the first instance we will address the precision, recall and F1-score followed by the accuracy, specificity and Jaccard index. We will study the coverage of the credible regions computed through the posterior distributions. Then we will discuss ROC curve, precision-recall curve and k-fold cross-validation. Finally we will conclude with a small discussion about what we could do with dependent samples.
Reproducibility Checklist
Software is based on the open-source bob.measure library. N.B.: Software leading to these results was only partially integrated into the bob.measure_ software stack.
No databases are required to reproduced results, which rely on Monte-Carlo simulations only.